When having a particle’s behavior depending on surrounding particles, using a proximity mesh is one way to reduce the combinatorial explosion of the relationships. With only 5 particles evolving onto an area, asking each of them to compute the distance to the others requires (5*4) distance computations: n*(n-1). Complexity is O(n²); not dramatic but still.

With 1000 particles, it requires almost 1 million distance computations; and such, many times per second. With an engine kernel running at 30Hz, it may needs roughly 10 millions distance computations per second. Only to check if two particles are close enough to activate a behavior. That never works in real time.

The first optimization consists of avoiding to recompute same distances. When particle A computes the distance to particle B, B should not redo it. This would divide the number of computation by 2 but, the storage of the result (and its retrieval) would becomes a problem.

The second optimization is to use a Proximity Mesh which divides the gaming area into a grid. Each cell of the grid lists all particles belonging to it. At a low rate frequency, the Mesh checks that each moving particles is still inside the cell’s perimeter. If found outside, the Mesh simply uses the coordinates of the particle to find the cell it belongs to, and moves the particle into its new cell.

Each particle now just have to make distance computations with the particles of the same list, plus those nearby, in case a particle is getting close to the cell borders.

In all cases, performances are drastically improved and real time (30Hz frame rate) can be reached, even with 30000 particles!

To speed up even more the simulation, the Mesh component can run on it’s own thread, on another CPU core. The engine kernel and the Mesh process then run in parallel.

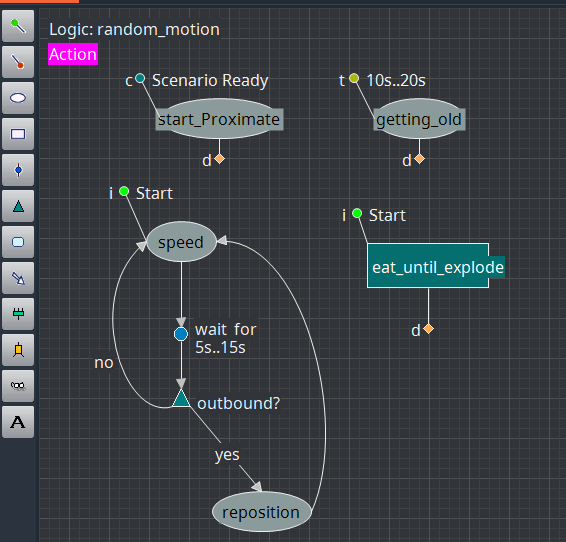
Behavior of the Particles

In this demo, each particle is moving with random speed and direction. At random time, both speed and direction are changed, iteratively. The obtained result looks like a Brownian movement.

At start, each particle is a newborn. After couple of seconds, each one may clump with any other according to rules explained below. The colors burst at the beginning (big bang) comes from the triggering of the rules, at the same time, for almost all of the particles.

Game Plan

Each particle (called A) does the following at every cycle (30hz):

• A moves at random speed and direction, for a random time, then repeat until clumped;
• if A is a newborn, it draws lines to all particles of the same color around;
• if A is not a newborn, it finds the closest particle B of the same color around, which is also not a newborn:
  • If the distance to B minus A+B radius, falls below a given value:
    • if A is bigger than B, B clumps to A, otherwise, A clumps to B;
    • if A and B are of the same size, a dice throw determines who clumps to who;
    • the size (radius) of the clumped one increases by 1/3 the size of the clumping.
  • if A radius gets above an obese value, color changes to fuchsia;
  • if A radius gets above a maximum value, A explodes and releases all clumped particles; they all become newborns and revert to their initial size;
• After a certain idle time, if A is still clumped, it explodes automatically.

The Mesh component does the following at maximum speed, on another thread:

• Processes all cells of the mesh grid:
  • For each particle A of a cell list:
    • if A position falls outside the cell perimeter, remove A from the list and use position (x,y) to find the cell A belongs to; add A to the new cell list.

    // auto burst 
    if (E:swallowed.count() > 2 && !E:explode)
    {
       if (!chrono.has("explode")) chrono.set("explode");
       else
       if (chrono.since("explode")> 30) {
          E:explode = true;
          chrono.clearAll();
       }
    }

    if (E:size > 20) {
       E:proximate->build_list = 2;
       E:proximate->display = true;
    }

    // size auto explode
    if (E:size > 30 && !E:explode) {
       E:explode = true;
       E:toggleColor();
       return AGAIN; // next cycle
    }

    // release all swallowed particles
    if (E:explode) {
       // Explode in small particles
       KArray<Entity>& list = E:swallowed;
       int stars = 2;
       while (list.count()) {
           Entity* e = list.pop();
           if (!e) continue;
           e->setPos(E:pos);
           e->setSpeed(RANDOM(100, 150), _m_s);
           e->setHeading(RANDOM(-180, 180), _deg);
           e->show();
           e->size = 5;
           e->young = 1; // newborn
           e->eaten = 0;
           if (stars) {
              e->proximate->build_list = 2;
              e->proximate->display = true;
              stars--;
           }
       }
       E:size = 5;
       E:explode = false;
       E:proximate->build_list = 0;
       E:proximate->display = false;
       E:resetColor();
       chrono.clearAll();
    }

Conclusion

Multi-threading is not the perfect solution to reduce the complexity of an algorithm but it helps. If the thread is running on another core, the result is good; if all share the same core, the multi-threading effect is not measurable.

The graphics (OpenGL) becomes also a high CPU consumer when the number of particles and connecting lines increases, mostly at high refresh rate (30Hz and more for the IG).

Increasing the number of threads (one per grid cell for example) is not helping at all; the CPU management of the threads suppresses all the benefits. The main vantage of a thread is to parallelize a process which cannot be (easily) time sliced from the code. When it can be done, embedding it into the real-time engine is a very good solution (which frees from the hassle of using semaphores).

A Proximity Mesh process is very easy to time slice from within the code, with a complexity of O(n).