Yann Takvorian
VirtualSim
Nice, France
yann@virtualsim.com
Submitted at Interservice/Industry Training, Simulation
and Education Conference (ITEC) 2019
Abstract
Driving a multi-body vehicle on a straight line is not challenging. Reversing with a 5 axles semi truck, going around corners or parking the trailer into a bay is far from being straightforward, even for a skilled driver.
In this paper, we will describe the process of building an artificial driver to autonomously handle various truck reverse parking situations, to assist or take over a trainee inside a simulator.
Introduction
This study is to provide an artificial approach to the gyration problem of an articulated vehicle in reverse, either to maintain a controlled trajectory or to park into a lot. For a human driver, it takes practice and experience to understand the turn radius and behavior of the articulated chassis, mostly when backing up, to avoid the jackknife phenomenon. Building a system which will mimic such behavior, after a learning phase, will address two different problems: the physics inherent to the vehicle motion and the maneuvers resulting from the driver’s skills.
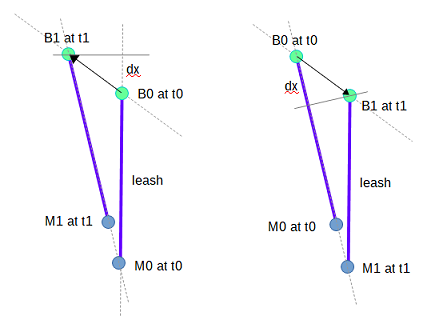
a tail (M) using a rigid leash.
The mechanics
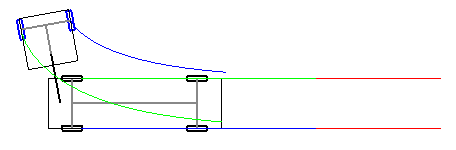
Pushing an aircraft backward or towing a trailer implies Newton laws and differential equations. Under a real-time simulation process which does not require trajectory extrapolation, a high frequency sampling of applied forces, torques and vector changes over time is sufficient to reproduce the motion of the steering axle [1] with good results. For the towed rear axle, the differential equation resolution using the tractor method [2] provides sufficient accuracy for our study (Fig.1). Under this approach it is effortless to introduce drifts or friction factors on tires according to twists, torque or even breakdown.
When driving forward, the front of the car (axle center of gravity) moves in the direction the wheels are facing. The rear axle (center of gravity) is towed by the drive shaft. The constraints on the back wheels are imposed by a fixed angle between the shaft and the rear axis (the chassis is perfectly rigid). Moving each points at every fraction of a second according to the projected speed smooths the motion of the whole body.
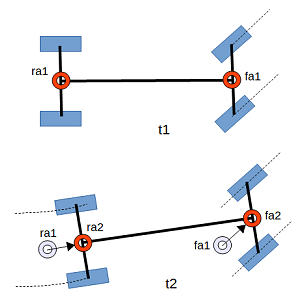
Figure 2 shows the position of the axles centers at t1 and t2. At t2, fa2, ra2 and ra1 are aligned. The result will be the same at t3, etc. If the steering angle does not change, the resulting ground trace of all wheels will be as in figure 2. The system is considered stable.
When reversing, the back of the body will go where the rear fixed wheels are pointing. So, the driving wheels (front wheels) have to steer in order to make the back wheels point to the correct direction. If the steering wheels are fixed and in absence of drift, reverse is symmetrical [3] (Fig. 3 & 4)
Because of the slow speed used and for the sake of simplicity, we will not consider drift [4]. If needed, it could be added into the Axle component. These drifts shall not change the result of the maneuvers as the control loops shall automatically compensate. This would not be the case if the paths were fully computed from mathematical formulas [5].
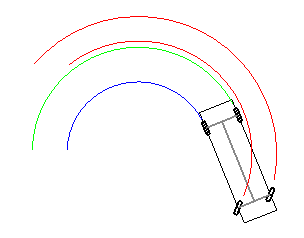
at constant steering angle
Using a trailer adds another level of separation and difficulty. When driving forward, the trailer will follow the rear vehicle axle and the tow bar will behave like a driving shaft. The system is unstable. To reverse such an articulated vehicle, the driving wheels must steer in order for the back wheels to point in a direction which will make the trailer wheels points in the correct direction. The system requires constant adjustment to avoid jackknife (a situation where the only escape is moving forward).
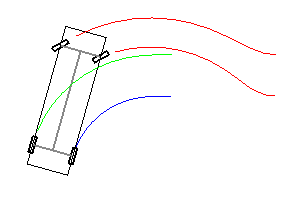
Automatic Driving
Reversing with a trailer is a complex procedure which needs training and practice in real life. For a synthetic model, two approaches can be considered:
- Mathematics approach with derivative functions
- Real-time empiric control-loop
For this project, we use the control-loop approach and develop an algorithm which constantly adjusts steering to keep the trailer over a specified path or towards a given point. A set of rules constantly checks the angles to avoid jackknife threshold and quickly reacts to resolve any drift.
Confronting the data
To ensure that our dynamic is physically correct, we need to measure the turn radius of each tire for a given steering angle and compare the data with the theoretical values. We will store the position of each tire during a full revolution (to get the circumference) then deduct the radius by a simple division. This empiric result will be used to position the gate and away points as we will see in chapter 7.
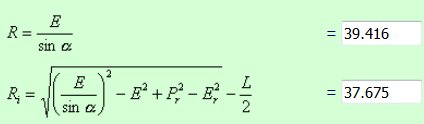
With L: 2.5 m, E: 6.2 m, steering angle: 10°, our simulation gives: R: 39.4, Ri: 37.6
When confronted with theoretical data, we can see that the sampling approach provides as accurate result as the mathematical counterpart (see figure 5).
Simple reverse maneuvering
In order to achieve a simple reverse maneuvering task, we use a rule-based mechanism to instruct the automatic pilot. These rules are intelligible and natural, the same as those we would give to a human driver.
Let’s define a point P in the area. If we want the vehicle to reach this point in reverse, by steering front wheels (limited in our case to 45°), the following 3 rules are required:
Rule 1:
if distanceToPoint() > 3 //meters
then
Vehicle.setSpeed(-2); // m/s
Vehicle.setSteering(-angleToPoint());
Rule 2:
if distanceToPoint() <= 3 //meters
then
Vehicle.setSpeed(0);For clarity, we are here using constant values. In real, distance threshold are function of speed and hitch angle.
Function distanceToPoint() returns the distance in meters between the point and the vehicle.
Function angleToPoint() returns the signed aperture between the azimuth to the point and the bearing of the rear of the vehicle. Note that we are steering with the negative sign as we need to reverse. If the given value is greater than the limit of the wheel angle, the maximum allowed is used.
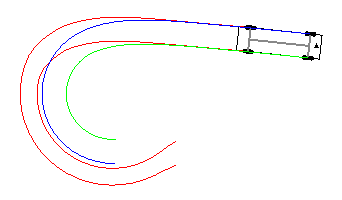
The two rules are combined into a Context object called goto_point and each rule reactivates itself 1 second after being triggered. Fig.6 shows the result of rules 1 & 2.
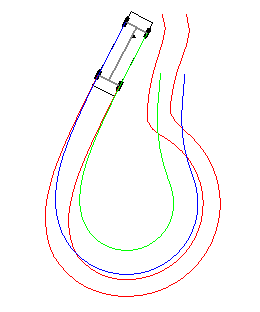
Unfortunately, this simple rule set fails when the vehicle is too close to the target point (Fig. 7). The same pattern would occur in real life and the obvious action would be to first get further from the point.
Let’s add a third rule to the context in order to solve the endless circling phenomenon (Fig 8):
Rule 3:
if abs(angleToPoint()) > 90 and
distanceToPoint < turningRadius()
then
Vehicle.setSpeed(-3);
Vehicle.setSteering(angleToPoint()/5);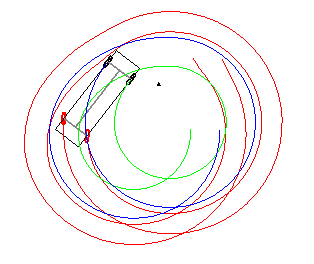
Rule 3 fires if the vehicle is too close to the target and is not approaching it. When triggered, the whole context reactivates itself after 3 seconds, freezing all rules and giving enough time for the vehicle to move away. Here is the result:
Adding a Trailer
With a trailer, rules mechanism is handling the general purpose. The most demanding job while reversing with a trailer is the control of the angle between the two body shafts to avoid jackknife. Once the angle is controlled, it is just a question of time and distance traveled before the trailer will head in the correct direction or towards the target point. A state machine logic is perfect to describe a tactic when the strategy is controlled by rules. The first process is the hands and the second is the brain.
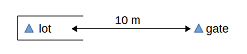
Two rules are necessary to prepare the vehicle in order to make it backup correctly and align. The first creates a gate point at a certain distance from the lot, aligned with it. In the experiments, values around two times the length of the trailer give the best results.
Rule 1: if (gate_point == null)
then createGatePoint(lot,10); // meters
Rule 2: if (gate_point and
distance(trailer,gate_point) < turn_radius)
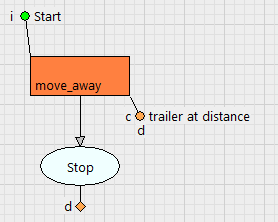
then moveAway(gate_point,15); // meters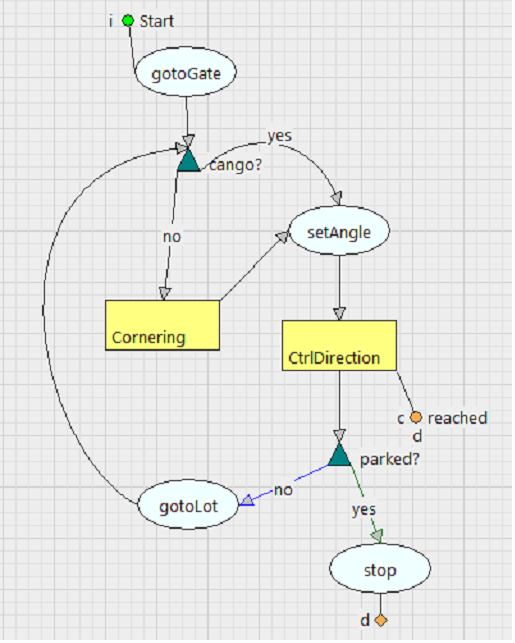
The createGatePoint function positions a virtual point at 10 meters from the lot, see figure 10:
If the distance between the trailer and the gate point is too short, or if the whole vehicle configuration and turn radius are not compatible, the tractor must get away. The moveAway function activates a special logic task which drives the trailer at 15 meters from the gate (these values are in real a function of the length and rate of turn of the full vehicle).
Rule 3:
if (gate_point and distance(trailer,gate_point) > turn_radius and vehicle.getSpeed() == 0)
then
reversePark(gate_point,lot);The reversePark function activates the logic figure 10.
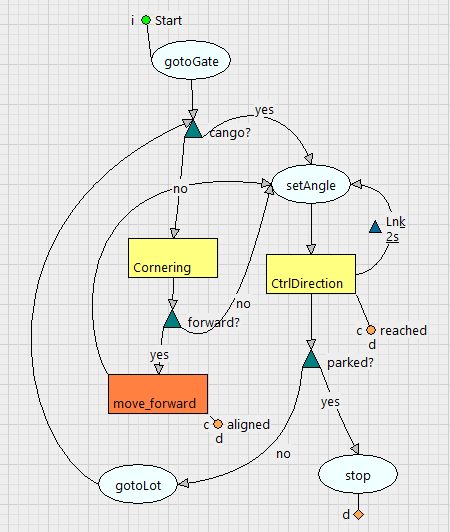
Two essential tasks for this maneuver are Cornering and CtrlDirection.
Cornering moves the trailer in reverse to make it head towards the point, while keeping maximum angle between the two shafts, and not exceed the jackknife threshold.
CtrlDirection maintains a constant trailer heading. This task only works if the trailer heading is below 15° range from the target heading. That is why the test cango is important as it decides between cornering and directing.
Finding the critical hitch angle
In order for Cornering to work correctly, the maximum hitch angle must be found. As a reminder, this angle is the limit beyond which the jackknife is unavoidable (configuration where the reverse motion must be stopped). Mathematical formulas exist [6] but the empiric approach provides good results using any tractor trailer dimensions. For that, Cornering is used iteratively with an increasing angle. As soon as the angle cannot be kept by steering the wheels, the jackknife threshold is found.
// Cornering task code:
if (phase == 1) {
vehicle.axle.setSteering(max);
float jnf = vehicle.axle.angleWithTrailer();
if (fabs(jnf) < maintain) {
maintain = 180-fabs(jnf);
phase = 2;
}
}
if (phase == 2) {
float agl = vehicle.axle.angleWithTrailer();
float sgn = SGN(agl);
agl = 180-fabs(agl);
vehicle.axle.setSteering(2*sgn*
LINEAR_INTERPOLATION((maintain-agl),0,maintain,0,max));
}Max variable stores the maximum steering wheels value in degrees. Maintain stores the angle to maintain (greater than the jackknife angle). 180° is perfect alignment of the two shafts. With this trailer and vehicle characteristics, 140° is the jackknife angle (below 140° angle cannot be maintained).
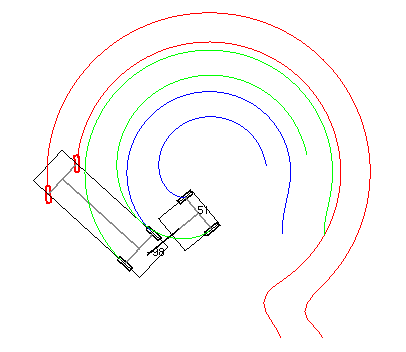
To be safe, the Cornering task runs at 0.98 of the threshold. A full convolution of the vehicle and trailer gives the maximum cornering radius that can be safely reached.
Once these two values are obtained from an initial learning phase, the vehicle can park its trailer on the lot from any position and orientation in the parking space.
The CtrlDirection task is also relatively simple:
float ag = getApertureToAngle(angle);
float ap = 180 – vehicle.axle.angleWithTrailer() + ag;
CHECK_180(ap);
vehicle.axle.setSteering(-2*
LINEAR_INTERPOLATION(ap, -20, 20, -max, max));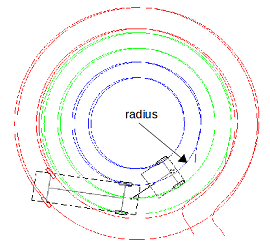
The formula uses empiric values. Higher or lower values make the steering more or less responsive.
In the code above, angle is the value in degrees the trailer must head. Max is the maximum steering wheels angle.
The three points algorithm
In order to find a practical solution to most configurations (if not all), a logic or set of rules must analyze the planar representation of the parking slot and orientation, versus the current position and orientation of the tractor and its trailer.
As the driving automaton has only one control-loop for the cornering and another one to acquire and keep a given heading in reverse, it needs direction. The slot point is where to park the trailer. It is essential to compute at least the gate point position to insure the alignment.
When the initial conditions do not allow the gate point to be properly reached, an away point must be inserted in the maneuver sequence, so that the gate point becomes easy to approach in reverse.
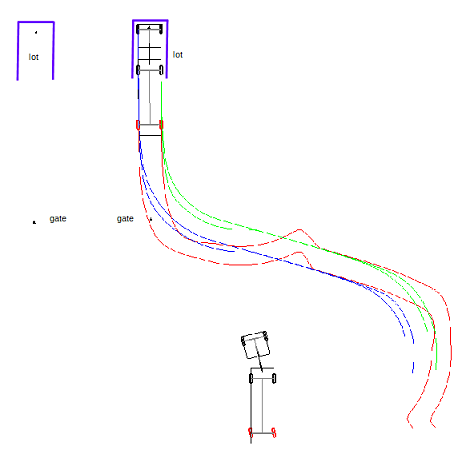
Fig. 15. Example of the maneuver to park
the trailer on the lot using the gate point.
The position of the away point depends on the position of the tractor, considering it must be reached in forward motion. In some situations, a U-turn is required (simple procedure with a cornering at maximum turn rate).
An example is given Fig. 15 with two cars + trailer A & B to park into the parking slot (fix point). The gate point must be positioned along the parking axis, at distance twice the length of the full articulated vehicle (rule of thumb).
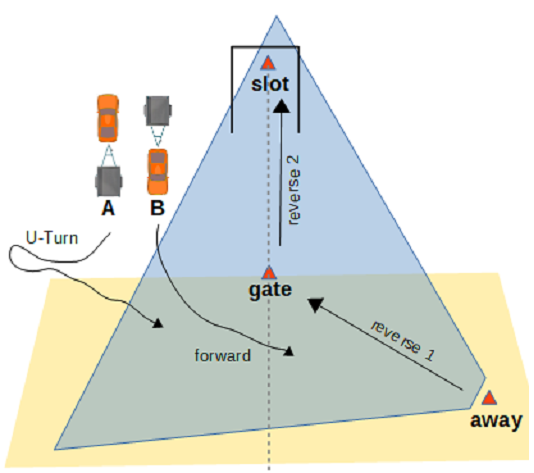
to A and B configurations
As neither the orientation of A or B allows reversing toward gate from inside the orange area (bottom), an away point must be used. Positioning the away point respects its approach cone (in blue) which is always oriented along the away–gate segment.
Away point must be reached in forward motion. A vehicle will need to do a U-Turn (simple procedure with a cornering at maximum hitch angle).
At gate point, the trailer must be aligned on slot point for the final reverse 2. So, cornering procedure must be engaged during the reverse 1 motion.
Long trailer truck
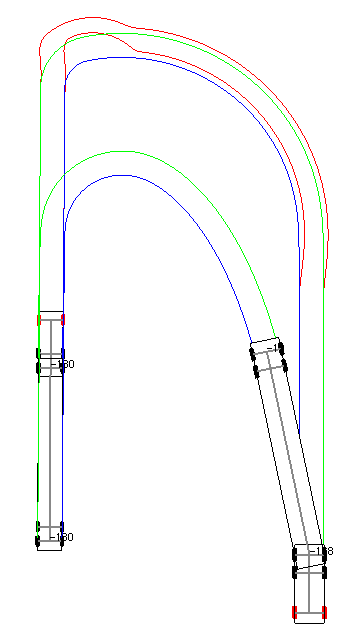
In previous work, a long vehicle parked a short trailer. Now, we are attempting the opposite: a truck tractor, 2 axles and a long trailer. The turn radius is different and the jackknife phenomenon is less of a concern since the kingpin is located over the tractor rear axle which can rotate with an angle fan of 180° or more [7].
Maneuvering in a constrained space
Contrary to a short draw-bar trailer which makes the control quite difficult, having a long trailer with a hook on the rear tractor bogie allow sharper U-turns (Fig 16).
The previous rules can be reused with minor modifications:
Rule 1: if (gate_point == null) then createGatePoint(lot,3);
Rule 2: if (gate_point and
distance(trailer,gate_point) < trailer.length())
then moveSideAway(gate_point, lot.orientation(), trailer.length());
Rule 3: if (gate_point and
distance(trailer,gate_point) > trailer.length() and
tractor.getSpeed() == 0)
then tractorReversePark(gate_point,lot);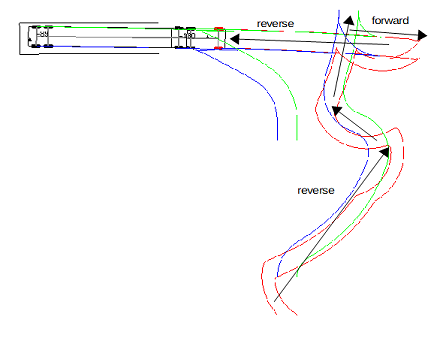
The moveSideAway function activates a special logic which position the truck at a given distance from the gate position and perpendicular to the lot (see figure 18)
The tractorReversePark function activates different logic that of the short trailer. The automate introduces a drive_forward task (in orange) to realign the truck on the last part of the parking phase, as seen on logic diagram figure 19.
The result of such logical sequence, based on angles and distances, and deciding when to move backward or forward (once the rules have put the truck in a correct configuration to solve the parking procedure), gives a practical solution as shown in figure 18.
Conclusion
This research on maneuverability of articulated vehicles demonstrates that using only angles, distances and control loops, was enough to develop an automaton behaving like a human driver, but in a more accurate manner as the control loops are based on real values and not on eye perception.
The combination of high-level strategic ruling based on three points and low-level tactical logic to sequence them proved to be an efficient way to address the problem [4]. Of course, the more rules and complex logic introduced would cover greater situations and configurations. Obtaining input from experienced truck drivers would also extend the system with more customary maneuvers.
In a truck simulator, if the trainee had visual cues computed by the software, showing the deviation of the steering according to the computed ones, he would realize perfect parking in difficult configurations. He could also learn from the system which could show him first how to perform a correct maneuver or correct him in real time.
Acknowledgments
Thanks to Alice Macklin, head of content – Defense and Security Clarion Events, for giving some more time to write this paper and review the content. Thanks also to ITEC Committee Member Paolo Proietti for the use of the MIMOS Conference template format.
All the simulations in this research run on vsTASKER software from VirtualSim.
Author/Speaker Biography
Yann Takvorian graduated from Computer Science Engineering in 1991. He studied Artificial Intelligence in Paris then obtained his first position at Airbus to develop computer-based courses for pilots. He has since spent his career in the simulation business as a presales engineer and consultant, which has taken him all over the world.
In 2004, he founded and still run VirtualSim, a company that develops and sells a scenario editor COTS product for real-time simulation and training systems.


